The Peano curves are amongst the first known fractals curves. They were described
the first time in 1890 by the italian mathematician Guiseppe Peano. Some confusion seems to exist for the authorship of some fractals curves so I decided to limit on the one showed in the book from Mandelbrot. Furthermore, the drawing method used is a free interpretation of the actual one ...
All pictures are from Acheron 2.0, a free explorer of geometrical fractals. You can download Acheron 2.0 here
Construction Back to Top
Start from a octogon drawn inside a square. Divide the octogon in nine
smaller octogons. Link the outer octogons two by two and then link all those
couples to the central octogon.
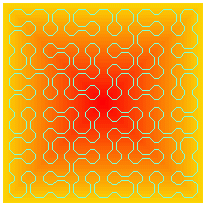
Here is what you get :
Applying the same procedure to the nine small octogon gives rise to the
drawing showed here:
Repeated several times, this procedure leads to a very intricate but
fascinating pattern. Note that repeating it more than 4 time is quite useless
as the curve segments start to merge and the aesthetical aspect vanishes ...
Properties Back to Top
- Fractal Dimension
- Self-Similarity
The fractal dimension is computed using the Hausdorff-Besicovitch equation (self-similarity method):
D = log (N) / log ( r)
Replacing r by three ( as each segment is divided by three on each iteration) and N by nine ( as the drawing process yields 9 smaller octogons) in the Hausdorff-Besicovitch equation gives:
D = log(9) / log(3) = 2
Looking at two successive iterations of the drawing process provides graphical evidence that this property is also shared by this curve.
All Variations described are available using Acheron 2.0
- Iteration Level
- Curve Style
Four recursion levels are available.
The Peano curve is a closed curve. The inner space can be filled to increase the contrast with the surrounding background ...
Born: 27 Aug 1858 in Cuneo, Piemonte, ItalyDied: 20 April 1932 in Turin, Italy
Giuseppe Peano was born in a farmhouse about 5 km from Cuneo. He attended the village school in Spinetta and in Cuneo. His uncle soom realised that Giuseppe was a very talented child, he took him to Turin in 1870 for his secondary schooling and to prepare him for university studies.
On 29 September 1880 Peano graduated as doctor of mathematics joined the staff at the University of Turin in 1880.
The following year he discovered, and published, a method for solving systems of linear differential equations using successive approximations, independently discovered by Emile Picard. In 1888 Peano published the book Geometrical Calculus which begins with a chapter on mathematical logic. This was his first work on the topic that would play a major role in his research over the next few years and it was based on the work of Schroder, Boole and Peirce. This book contains the first definition of a vector space given with a remarkably modern notation and style and, although it was not appreciated by many at the time, this is surely a quite remarkable achievement by Peano.
In 1889 Peano published (in Latin !!!) his famous axioms, called Peano axioms, which defined the natural numbers in terms of sets. This was considered at once as a landmark in the history of mathematical logic and of the foundations of mathematics.
He invented 'space-filling' curves in 1890. Hausdorff wrote of Peano's result in Grundzege der Mengenlehre in 1914:
This is one of the most remarkable facts of set theory.
From around 1892, Peano embarked on a new and extremely ambitious project, namely the Formulario Mathematico. The project was completed in 1908 and one has to admire what Peano achieved but although the work contained a mine of information it was little used.
Even before the Formulario Mathematico project was completed Peano was putting in place the next major project of his life: finding a universal language. In fact the final edition of the Formulario Mathematico was written in this artificial language which is another reason the work was so little used.
Peano's career was therefore rather strangely divided into two periods. The period up to 1900 is one where he showed great originality and a remarkable feel for topics which would be important in the development of mathematics. His achievements were outstanding. However this feel for what was important seemed to leave him and after 1900 he worked with great enthusiasm on two projects of great difficulty which were enormous undertakings but proved quite unimportant in the development of mathematics.
Biography From School of Mathematics and Statistics - University of StAndrews, Scotland