The Minkowski Curve is also called the Minkowski sausage. According to
Mandelbrot, the origin of the curve is uncertain and was dated back at least to Hermann Minkowski.
Construction Back to Top
As almost all fractals curves, the construction of the Minkowski curve is based on a recursive procedure.
At each recursion, a 8-sides generator is applied to each line segment of the curve. As the first step starst with a straigth line, it gives:
First Iteration in Minkowski Curve
Note that there are 8 differents segments (and not 7, as it can be thought at first sight ..)
The same generator is applied to the 8 segments formed at the first iteration to produce a somewhat more complex curve:
Second Iteration in Minkowski Curve
The third iteration already gives a nice picture:
third Iteration in Minkowski Curve
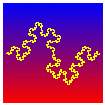
The first stages of the procedure modify heavily the appearance of the curve. However, quite soon, the curve remains roughly the same whatever the recursion level, only the time required to drawn the curve increases.
Properties Back to Top
- Curve Length
- Fractal Dimension
- Self-Similarity
The length of the Minkowski curve increases at each iteration. On each iteration, the length of the segments is divided by four and the number of segments is multiplied by eight, hence the total curve length is multiplied by 2 with each iteration.
Obviously, the length of the curve tends to infinity as the iteration number increases.
The fractal dimension is computed using the Hausdorff-Besicovitch equation:
D = log (N) / log ( r)
Replacing r by four ( as each segment is divided by four on each iteration) and N by eight ( as the drawing process yields 8 segments) in the Hausdorff-Besicovitch equation gives:
D = log(8) / log(4) = 1.5
Looking at two successive iterations of the drawing process provides graphical evidence that this property is also shared by this curve.
All Variations described are available using Acheron 2.0
- Iteration Level
- Basic Geometric Figure
Instead of starting with a straight line, the drawing can start from a triangle or a square, leading to interesting curves.
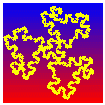
Five recursion levels are available. Above this iteration number, the overall aspect of the curve remains essentially unaffected.
Born: 22 June 1864 in Alexotas, Russian Empire (now Kaunas, Lithuania)Died: 12 Jan 1909 in Gottingen, Germany
Hermann Minkowski studied at the Universities of Berlin and Konigsberg. He received his doctorate in 1885 from Konigsberg. He taught at several universities, Bonn, Konigsberg and Zurich. In Zurich, Einstein was a student in several of the courses he gave.
Minkowski accepted a chair in 1902 at the University of Gottingen, where he stayed for the rest of his life. At Gottingen he learnt mathematical physics from Hilbert and his associates.
By 1907 Minkowski realised that the work of Lorentz and Einstein could be best understood in a non-educlidean space. He considered space and time, which were formerly thought to be independent, to be coupled together in a four-dimensional 'space-time continuum'. This space-time continuum provided a framework for all later mathematical work in relativity.
Minkowski was mainly interested in pure mathematics and spent much of his time investigating quadratic forms and continued fractions. His most original achievement, however, was his 'geometry of numbers'.
At the young age of 44, Minkowski died suddenly from a ruptured appendix.
Biography From School of Mathematics and Statistics - University of StAndrews, Scotland