Ernesto Cesaro, an italian mathematician, described several curves that now bears his name. The curve showed below, dated back to 1905, was used by Mandebrot in his work on fractals.
The Cesaro curve is a set of two curves with intricate patterns that fit into each other.

Construction Back to Top
As almost all fractals curves, the construction of the Cesaro curve is
based on a recursive procedure.
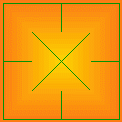
To draw the cruve, start with a square. Draw the first half of the four
diagonals starting from the center of the square. Draw the first half of the
four medians starting at the edges of the square.
The first iteration gives the following picture:
The procedure is the repeated with the squares obtained by
dividing the original square in four sub-squares.
The second iteration already gives an idea of the interweaving of the two
curves:

The third iteration already gives a nice picture:

Intricate patterns arise on subsequent iterations. However, quite fast,
the area covered by the curve increases up to the point where it occupies the
whole area.
Properties Back to Top
- Fractal Dimension
- Self-Similarity
The fractal dimension is computed using the Hausdorff-Besicovitch equation:
D = log (N) / log ( r)
Replacing r by two ( as the square side is divided by two on each iteration) and N by four ( as the drawing process yields four self-similar objects) in the Hausdorff-Besicovitch equation gives:
D = log(4) / log(2) = 2
Looking at two successive iterations of the drawing process provides graphical evidence that this property is also shared by this curve.
All Variations described are available using Acheron 2.0
- Iteration Level
Eight recursion levels are available. Above this level of iteration, the drawing area is covered more and more completely by the curve.
 Born: 12 March 1859 in Naples, Italy
Born: 12 March 1859 in Naples, ItalyDied: 12 Sept 1906 in Torre Annunziata, Italy
Ernesto Cesaro studied in Naples, then in Liège going after some time to Ecole des Mines of Liège. He received a doctorate from the University of Rome in 1887. Cesaro held the chair of mathematics at Palermo until 1891, moving then to Rome where he held the chair until his death.
Cesaro's main contribution was to differential geometry. This is his most important contribution which he described in Lezione di geometria intrinseca (Naples, 1890). This work contains descriptions of curves which today are named after Cesaro.
In addition to differential geometry, he worked on many topics such as number theory, divergent series and mathematical physics.
Biography From School of Mathematics and Statistics - University of StAndrews, Scotland