Features of DLXSolver 2.0
- Preview of Board Solving Process
- Sudoku Boards
- Entering Sudoku Boards
- Solving the Sudoku grids
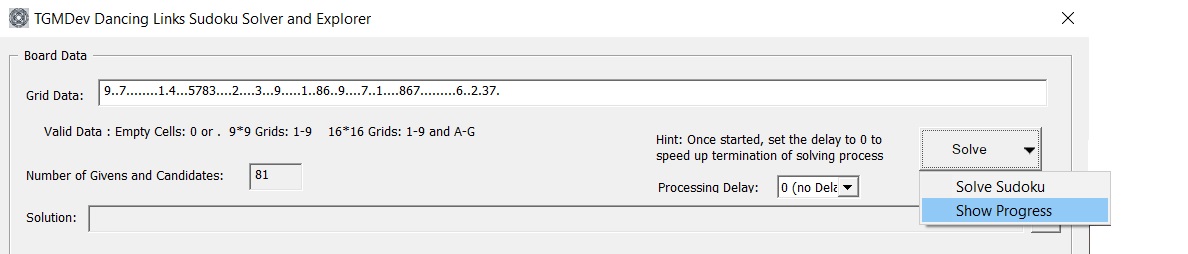
- Solve Sudoku: this is the fastest mode. The grid is solved using the Dancing Links method and only the complete solution is displayed.
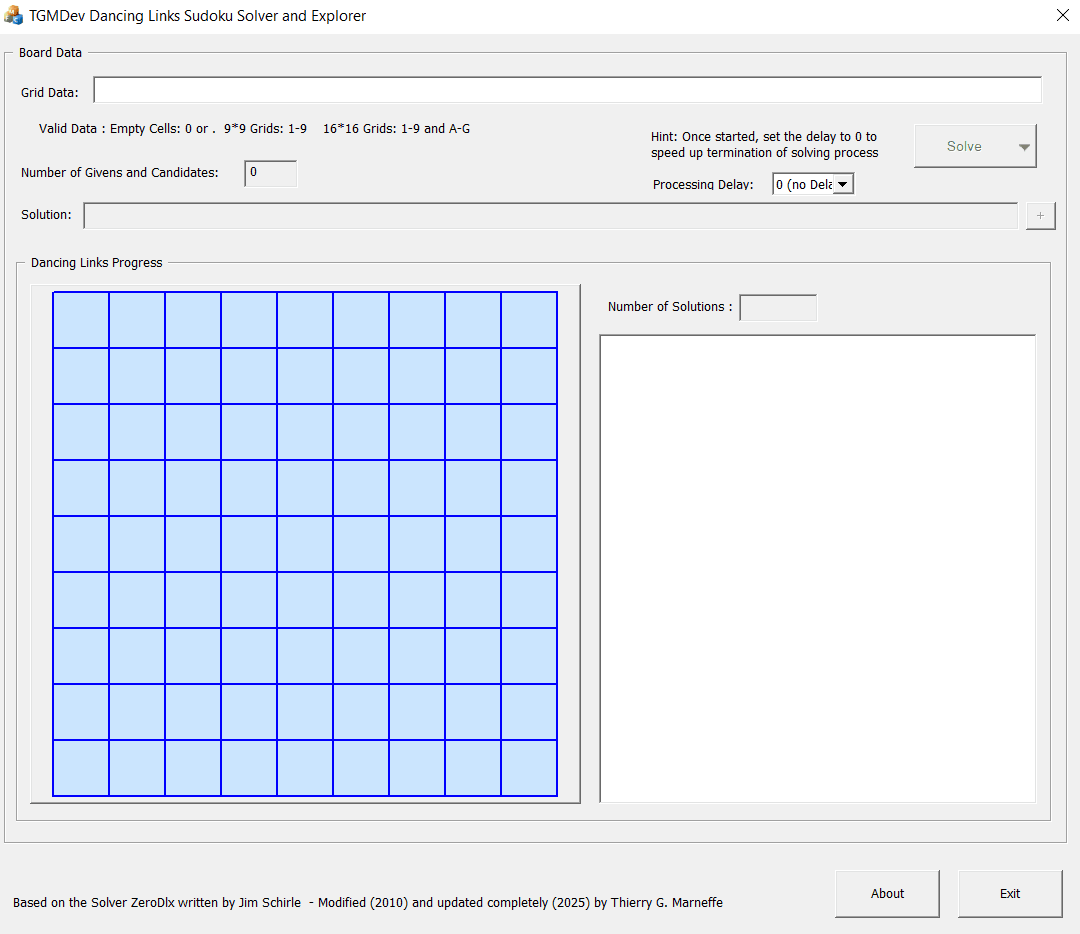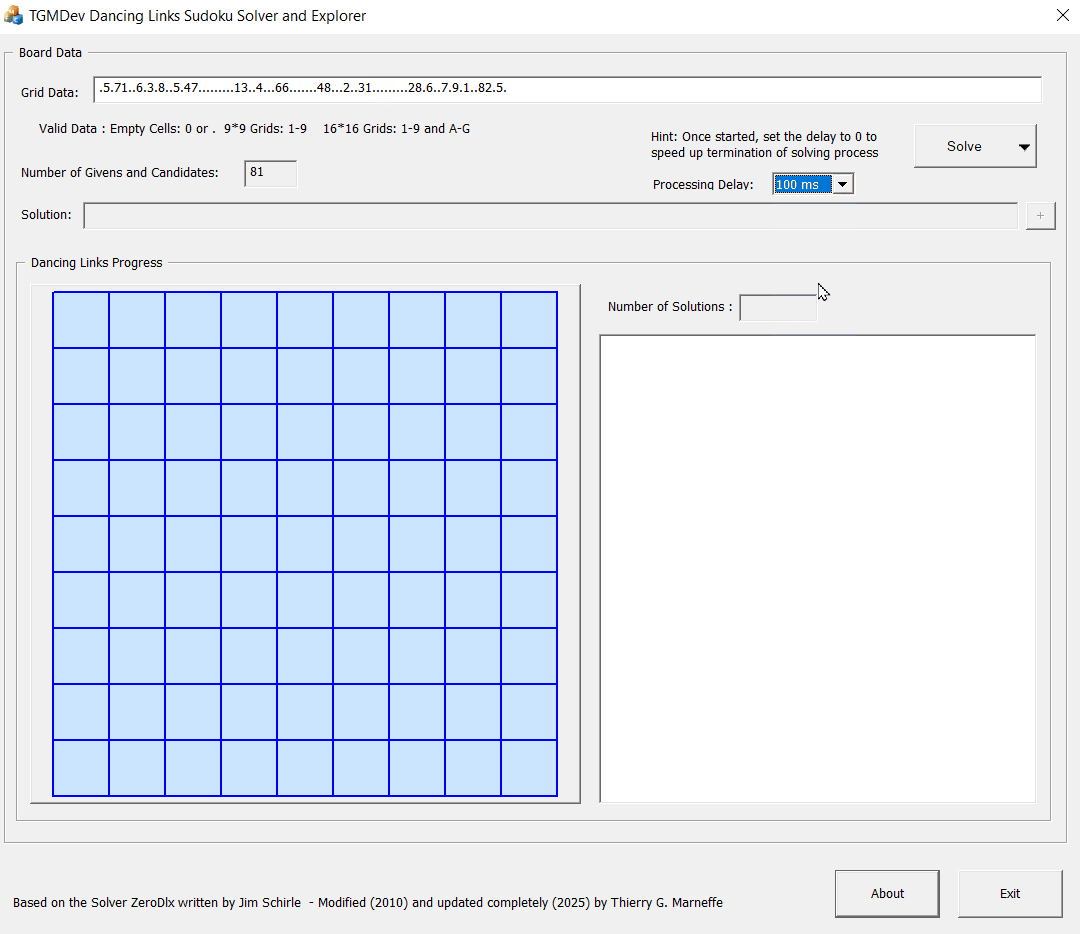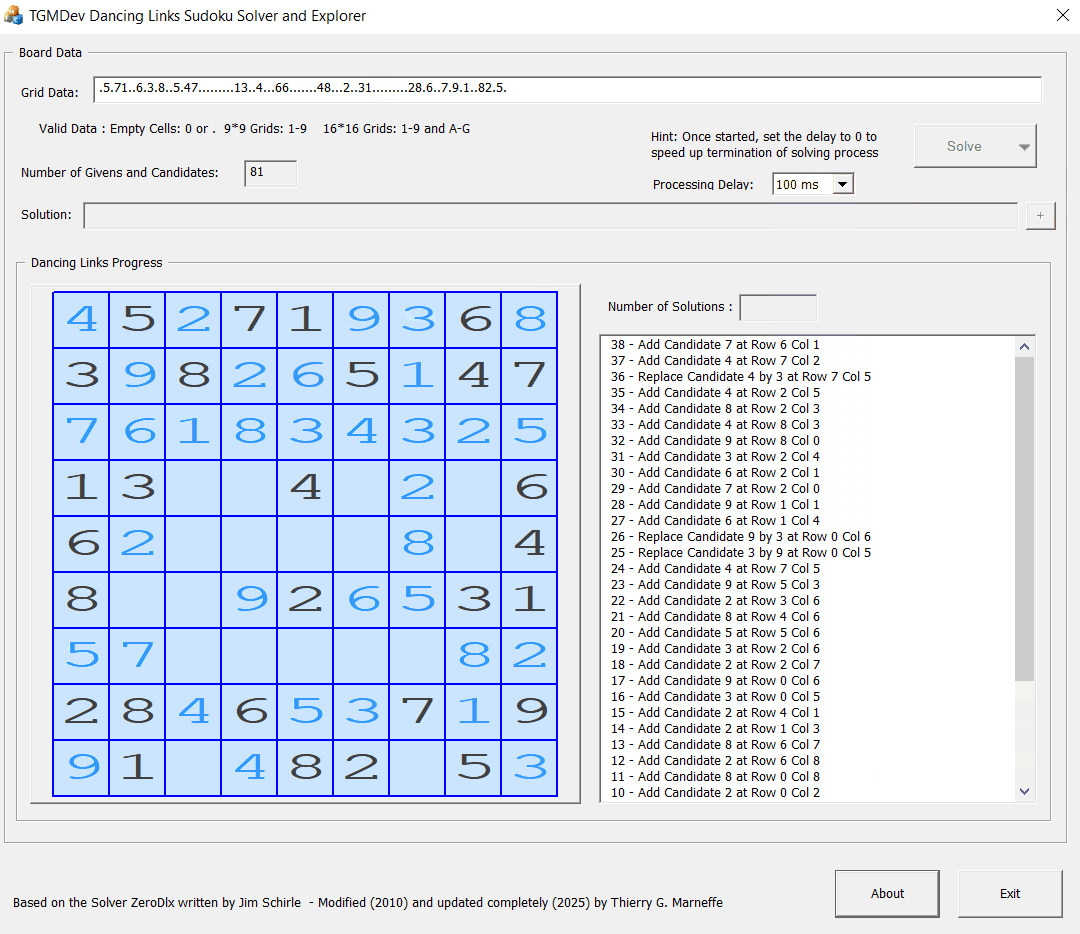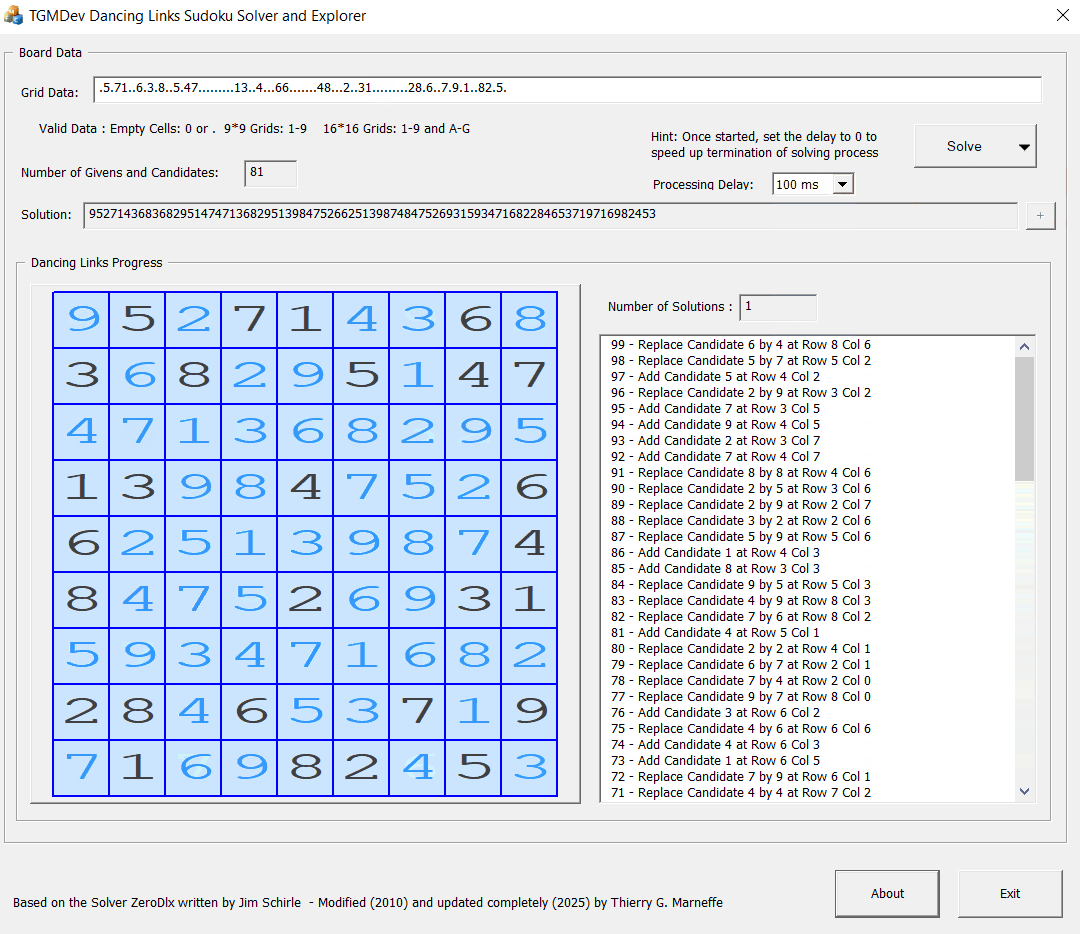
- Show Progress: this processing is a little bit slower as the progress of the solving process is shown on screen by updating the baord and the list box (see more below)
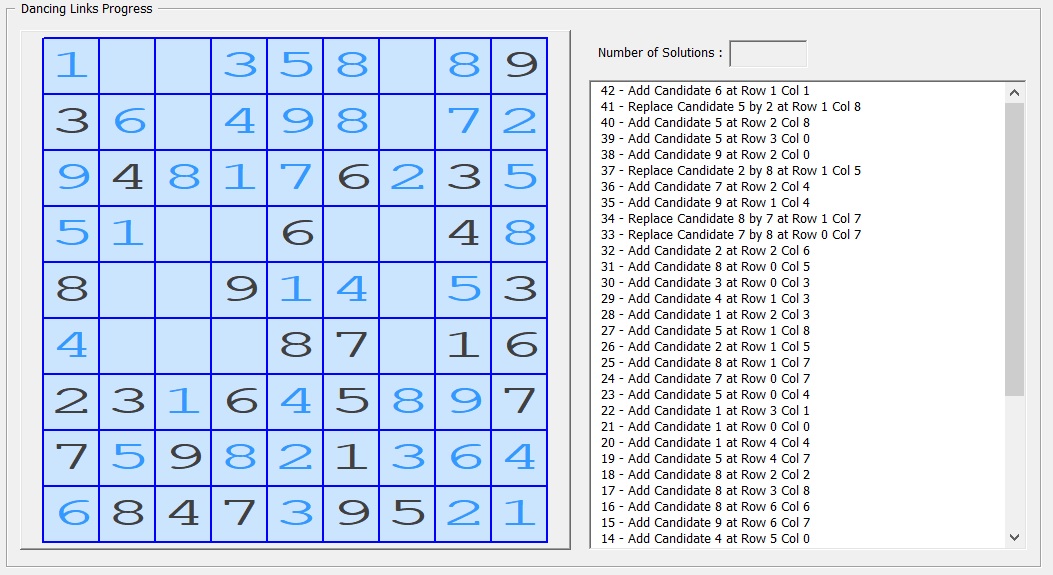
- Sudoku Solving progress
- the Sudoku board by updating gradually the different candidates (in blue color) to the board.
- the action list by adding the actions defined by the solver: either a candidate addition or a candidate replacement. The last actions are always on the top of the list.
- Solver processing and Boards Difficulty Level
Here is a dynamic display of the solving process as you can see it with DLXSolver 2.0
This animated gif is build using the powerful tool ScreenToGif .
DLXSolver 2.0 supports 9 x 9 and 16 x 16 Sudoku boards.
Just as a fast reminder... Sudoku Boards are made up of cells (81 cells in a 9*9 Board and 256 cells in a 16*16 Board). Boards are divided in Rows (horizontal lines), Columns (vertical lines) and Boxes containing 9 (3*3) or 16 (4*4) cells. The rows, columns and boxes are called Groups. Every group must contain all the numbers from 1 to 9 (in 9*9 Board) or from 1 to 9 and A to G (in 16*16 Board). At the start, some cells are filled with numbers called Clues or Givens. The numbers added when solving the game are called candidates, solved cells or Quest.
The givens of the Sudoku boards are the numbers from 1 to 9 (in 9*9 Boards) or from 1 to 9 and A to G (in 16*16 Boards). The empty cells or candidates are filled with . or 0.
The grids can be entered manually or pasted from the clipboard. The installer of DLXSolver 2.0 adds several text files containing grids with different levels of difficulty. These can be used with the DLX Solver.
An other possibilty is to generate the grids with the freeware TGMDev Isanaki Sudoku and copying the grids to the clipboard.
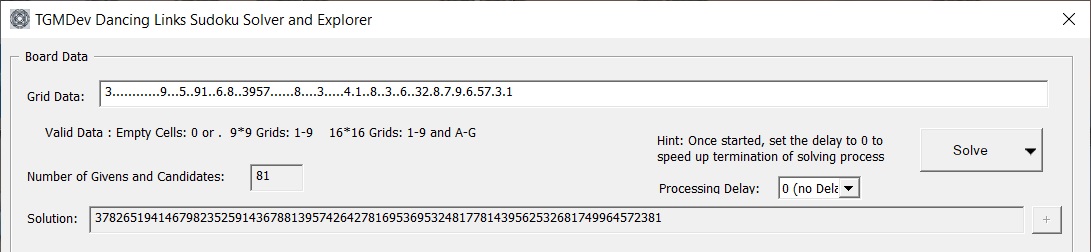
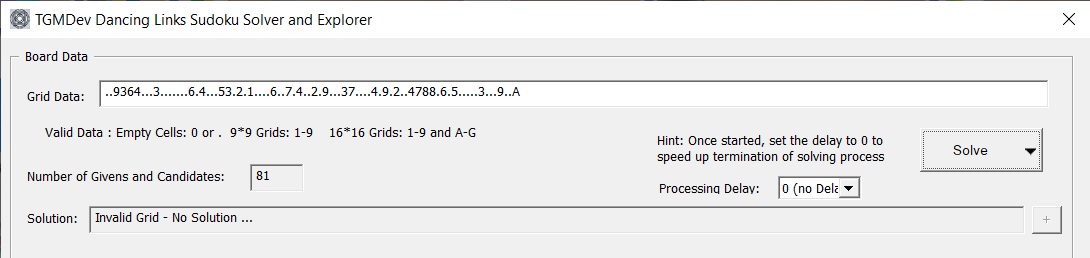
Any other characters than the valid givens (as the last character A in the exemple below) will interrupt the solving process and genereates an invalid grid with No Solution.
The button 'Solve' is enabled only if the entered grids contain exactly 81 or 216 characters.
Once a valid grid is entered, the button 'Solve' is enabled.
Two modes of solving are available:
The Solving progress mode can be tailored by changing the Processing Delay (from 0 ms to 1 second). This gives the opportunity to visualize the progress of the solving process eaisly.
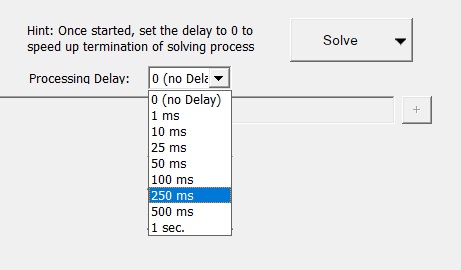
Here is the hint: Set the delay to 0 ms while the process is running will speed the termination of the solving process.
In Solving Progress Mode, DLXSolver 2.0 updates:
For very simple grids, the solver performs only simple candidate additions. There is no backtracking that requires to re-process the grid and proceed with the replacement of a candidate already placed on board. But hard-to-solve grids require backtracking and several actions of candidates replacement.
If you look a the solving process in slow mode (1 sec delay), you can see it clearly with the following grid:
.4........2...61.5..61...7.1..8.....3.2.4.8.6.....9..7.6...49..9.52...6........8.The relationship between grid difficulty level and solver processing has been tested with grids generated by the freeware TGMDev Isanaki Sudoku. Grids with increasing difficulty levels and different symetries were tested with the DLXSudokuSolver.
The results, obtained on 23 march 2025 using DLXSudokuSolver 2.0 and Isanaki Sudoku 2.6b , show that as the difficulty level increases, the solver makes more candidate replacements. This relationship is not always respected but this may be due to the subjective level of difficuly, based on the use of increasingly complex human resolutiong strategies to find the candidates.
| Difficulty Level | Symetry | Grid | Givens | Cand. | Add. | Repl. |
|---|---|---|---|---|---|---|
| 9 * 9 grids | ||||||
| Very Easy | Symetrical | 61...9.8....2.35...3.....195.8.9.4.7.......9....6...52...85..63..6..18.......79.. | 28 | 53 | 53 | 0 | Very Easy | Non-Sym. | .....52.6..61..43..593...8.....713.....453.....729.....1...472..72..85..5.49..... | 31 | 50 | 50 | 0 | Easy | Symetrical | 3.2...8....96...7....1.5....16.5....9.....28.7....3....2..67...8..32......7...9.. | 24 | 57 | 57 | 0 | Easy | Non-Sym. | ....2.6.3.....18..4.5...72.1....6.828...7...435.8....6.17...9.8..83.....2.3.9.... | 29 | 52 | 52 | 0 | Medium | Symetrical | ....1....96...73.2....4..7..9.8.1.3..3.2.....7.5......2......4......9..88....3769 | 25 | 56 | 56 | 0 | Medium | Non-Sym. | 1....76...8.......7.51.9.....1...4.66.45.31.73.8...5.....3.69.4.......7...74....2 | 28 | 53 | 53 | 0 | Hard | Symetrical | .81.....4...7.......6..2.8..7..9.4....31.....5....31...57.1.82....3..9....2...3.. | 24 | 57 | 57 | 1 | Hard | Non-Sym. | .3..4..21......67...7...453.439..2.....462.....6..374.754...3...91......86..3..1. | 31 | 50 | 50 | 0 | Very Hard | Symetrical | ..7.3..9...8.....4..97.5.38.9....6.....526....13.74...3...5.4....6.......51.8.... | 26 | 55 | 55 | 14 | Very Hard | Non-Sym. | 1..4....2....5..34..8.1..7..7.9.....3.58.79.1.....2.6..1..8.7..45..2....8....5..6 | 28 | 53 | 53 | 6 | Fiendish | Symetrical | ..8..73....26...5...6..19...1.98...6......8.5.9....4.........7.3.4..5....6..32... | 24 | 57 | 57 | 49 | Fiendish | Non-Sym. | .4........2...61.5..61...7.1..8.....3.2.4.8.6.....9..7.6...49..9.52...6........8. | 25 | 56 | 56 | 79 |
| 16 * 16 grids | ||||||
| Very Easy | Symetrical | .....2.E....57.F9..7..4..25A6.D.....95..G7.B..A...2A.3.791.E...8...B....3.A1.F.C7....G....D......4DEB96......85.2.F...3A59..1.E.B.9G..8...3.7.F..7.5.E.B2F.94.3.D..2....CEG...6B..4.7.536.1...G.E57..F...3C8.D46.B61ED79.A2G.3..GCA.361.BDE.F92.3..D..C.769.A.1. | 123 | 133 | 133 | 0 | Very Easy | Non-Sym. | 21E..5B......G6...F.E.7ABD....24..G9.28.51...DA.B..A6.9..2.F3178C.12.B5.63.7G.....8D..1.F...E..5.....DG6E5.8AB.25B.4...E..DG...78...BF..G...2.D99.572.C148B.....A..F...D.9..C4.....G9.47.FC.65.114C65.D..E.27..3.92...3C.48.DA..G8....A2D6.5.F...A7......G9..25B | 128 | 128 | 128 | 0 | Easy | Symetrical | 3B8.26.9.G..EDF.4.A...8C.EFD6......6.EGA.8.9....2....4FD36CAB.1..C....A..2....7F7..D...2.A8G5.....4.F..56..192.....F...E..3C8BD...C1A23.....D9.E......BFA.23.6.5EA.5D9.G81B..C27FG2...57D94.A......B..2.E....AG8G5..8A9.C.6.1..D..DA1..4..GBC.62.F...D.6..A834.. | 127 | 127 | 129 | 0 | Easy | Non-Sym. | .....G...93A47F.19CF.823......6...D.79...82..3.G3BG..E..4D.C.829.13G..C..57.FB.87..E138.DGB2A9...2A.B....14...3.9.B......3.....22.....7......D.F.G...1A....D.48...48FD9E.6173..BB.79.25..A..6C1.CF2.A.EG..9..6B3D.6..B1...E4.F...4......BFD.G275.79B8FD...A..... | 124 | 132 | 132 | 0 | Medium | Symetrical | .3.A18.6.C....GE57.C3.F..8...A6D6.GD5..73A..148.8..E.CD..G6..9...E.B..157......G3.8.C62B5.E....A.D.4..G.231.6.5..F...D9........BA.....5D......F...7964.1....A...D6B.....A...57.1.8..27AGC......4.2.3D56AE1...C9F.....B4.F.GC.6.2....G.8.49.3E..5..E..27F.B5A.14. | 119 | 137 | 137 | 0 | Medium | Non-Sym. | .A.....6F........G7D..B..9A.6.4.6.93.4..BE.2D.58.BE418D....G..C.4.G18.C3.5...72.32.57F.1.6GA9.E.D..7.2...F1......6.9DGEB.2............3.2DB4A.9......9F...6.C..B.3.B2C1.A.F7E.65.D6...8.C1.324.7.4..5....7D1GEA.E5.2B.7F..8.39.C.7.A.12..B..458........85.....7. | 122 | 134 | 134 | 0 | Hard | Symetrical | .62..9...E.CBF.A...92...FA....4.48.F1.5A2..D3C.....C.3.D14B9.......G..3.9D8.A4.C6.9..24..FA38.B...A..1.B....F5..8.35.ED.71..629.9256....G.1.D..7.1.7G....93F..C.BEF.9....C27G...G...F.17.5.A.....G62BA.......9D5D34.E.6..795.B....7....9B8D..G6.E..B...1.G..4.A. | 121 | 135 | 135 | 0 | Hard | Non-Sym. | 7A19B.G....8F.DC2.35.D9.6......G8C4E1.F37.9...2.6..F8..E..1A.3....C.3.B...A5..GD3.E..7.5.........8FB...D27.....35..G28E.31...7A..57...AC.FD21..EA.....71C...3D8.........G.7..C.ACG..DF...A.E.B....9.A2..4..3G..5.2...3.7BD.6A918F......G.25.4E.6G4.6E....9.FD237 | 122 | 134 | 134 | 17 | Very Hard | Symetrical | .D..94..FGE....C.C2...3169DB4..F..5F.....7.........GA.BF8...7.2..8F7..6GD1..34AB9.E....7CAB.D.G..6..F.E54...19....GC......F..87.7..5.6G....F.....4.921.A5D6.C.F.....D.4.BE8....6D...5.FB721.A.8..7186FD...A9.23.F543..18E.7.....G9.D3..4...8E..1....G...3...F... | 117 | 139 | 139 | 26 | Very Hard | Non-Sym. | 1..2....7C9.EG...GC.9..ABE.276.14FB...E.1...9...9.....GCA.F.4...5.DBA..6.24..E78.24.E1.8.5.....G8...G57.6.DE..24.3G.C..F8..B..D...1D....46..G..EB.245F..CA.G.7.9.8.....4.7...2B..A....CG..B.....245..C...FA...G7.E..3..12458C.6AFB....87..C129E5G.....5.9B....1. | 120 | 136 | 136 | 74 | Fiendish | Symetrical | 1.A2.8.E.C....D338B51.9D7.6.....4.C.A.52..D..8..7..964....A2..B....37C..4.GB...2.2.4..D.37....G.A..B4.69.1.D378F5....G.....E4.6DB5...DG.E.F.C3......EA1.B.....9G.498.......3.5.EE67..53...2...18...1D7..6.E4..3....DF......79.4C.B4EG...CD..86..8C.7.E.......D.1 | 116 | 140 | 140 | 236 | Fiendish | Non-Sym. | 2.G...6C....5.....E.41D.372..G.A6FA....E..DG4.7......BG.5..8.....4...G.B2DEFA.8...3A..1.C.5...B2.E.B..58.1.3.DG.CG...6..9A8B7......4F8C3..9...2G.59.D.B.A6..8.3.B2...7.6.8..D5...8.3529GF.B...A.....8..5.2F......9.5B3..8....2FDF.8..D79.315.C.....D....74...8.1 | 116 | 140 | 140 | 211 |